Daily 4 and Weekly 2: Tessellations

If we have a plane that we tile entirely with various geometric shapes, we have created what is called a tessellation. The most interesting tessellations are those which have a recurring pattern. Such tessellations are seen in a variety of situations, ranging from art to biological structures. These can be either two- or three-dimensional, or, theoretically, in even higher dimensions. As a simple example, given a moment's thought, we can clearly imagine a 4 by 4 unit square being tessellated with 16, 1 by 1 unit squares, and a 2 by 2 by 2 unit cube being tessellated with 8, 1 by 1 unit cubes.

One of the more interesting tessellations found in nature is the honeycomb. As it turns out, the design of the honeycomb provides the most efficient amount of storage space for the amount of materials used to create it. We know that, for a given perimeter, the most efficient shape in terms of area is the circle. That is, for a set perimeter, the circle has more area than any other shape. It then seems that honeybees may wish to create their honeycombs using circles, but this is not what we see. Instead, what we see is that honeycombs are hexagonal, and the reason for this has to do with tessellations.

We can easily see that circles cannot tessellate a plane. There will inevitably be gaps between the circles if we try to cover a plane with them, as seen below. From an efficiency standpoint, creating a honeycomb using circles is sub-par because both resources and space are wasted.

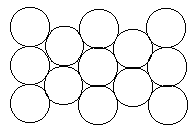
The goal of the honeybee is to then find the regular polygon that satisfies these criteria:

1. Forms a regular tessellation. That is, it can tessellate a surface by itself, and
2. Is as close as possible to a circle, meaning that more sides is better than less.

As it turns out, the only regular polygons that can form a regular tessellation are the equilateral triangle, the square, and the hexagon. Since the hexagon is the closest approximation to the circle from these shapes, it is the solution to all of the honeybee's woes.

Since the hexagon is the regular polygon that best approximates the circle and tessellates a plane, there is no wasted wax in constructing the honeycomb and the storage area for honey is maximized. Pretty cool, huh?

In addition to nature, tessellations can be found in our buildings. Extravagant tilings are found in Roman architecture, mosques, and even textiles.

(Doing Math) Using this website I found, I created the tessellation below.

It was more difficult to create an interesting pattern that would tessellate than I anticipated. I began by simply creating various patterns with the given shapes, without giving much thought to how the pattern would work on a macro scale. Because of this, the geometries of many of the patterns I tried would not tessellate. After realizing I couldn't simply make any pattern work that I wanted, it was necessary to take a more mathematical approach. I knew that the equilateral triangles could form a tessellation, so I first made a pattern that took advantage of this fact. This ended in me making the equilateral triangles shown above with the yellow hexagons in their centers.

I thought it would be boring to simply repeat this pattern to create my tessellation, so I added the orange lattice structure, more easily seen in the edges where the tessellation is incomplete. I knew six of the equilateral triangles I created could be used to form a hexagon, and I knew that hexagons can also tessellate a surface. As a result, I decided to create a lattice structure based on the shape of a hexagon. Voila!