Daily 6 and Weekly 3: Cube from Class and a Miscellany of Mathematics

In class, we were to build a cube that is broken into three parts: one part that consists of half the volume of the cube, another that is one third the volume of the cube, and a final piece that is one sixth the volume of the cube. I began with a drawing of the cube, and used it to determine how the three solids should be made.

The drawing got a bit hard to follow after drawing the triangular prism, so I had to move quickly and begin making the solids before I forgot the shapes I meant to draw. Here is a picture of what I came up with:

The pieces consist of a triangular prism (half the volume of the cube), a square pyramid (one third the volume), and a triangular pyramid (one sixth the volume). Determining the shapes to construct was rather straightforward: I began by creating the prism, since it pretty clearly is half the cube. We learned in class that the volume of a pyramid is one third times the base times the height, so I knew that this would be our choice for the piece that consists of one third the volume of the cube. However, determining how to make the pyramid so that we can still complete the cube with one more piece consisting of one sixth the volume took some thought. Clearly, the "top" vertex of the pyramid could not lie over the middle of the base, since it would not fit with the other required pieces to complete the cube. So, the vertex must lie on the same plane as one of the edges. Using the same argument, we see that the vertex cannot be on any arbitrary point on this plane; the vertex must be placed over a corner of the base. This construction is the only one which would allow us to easily build the cube with only one more piece. Combining the triangular prism and the square pyramid, we see what we must construct next to finish the puzzle.

We know if we create the final piece that it must necessarily be one sixth the volume of the cube, since the previous two combined account for five sixths the volume. Constructing this triangular pyramid was difficult, but combining it with the other two pieces completes the cube.

Here are the "cutout" versions of the pieces used to make the cube, created in Geogebra:

The triangular prism:

The square pyramid:

The triangular pyramid:

Many people seemed to have trouble with the triangular pyramid. It took me a moment to determine how it should be constructed, but then I realized that it would simply be half the square pyramid and so making it became much easier.

What I took away most from this activity was solidifying my understanding of the formulas for solids, particularly for the pyramids. I have never taken a geometry course other than in high school so I never gave much thought to the formulas, much less the fact that the formula may work for pyramids with a base of any shape.

Special Numbers (Communicating Math) and Proof of Closed Form for Sum of Natural Numbers

In class, we learned about particular sets of numbers that are "special" or "rare". For instance, we learned about perfect numbers like 6, whose proper divisors sum to that number. That is, all the divisors of a perfect number, excluding the number itself, sum to the number itself. If we continue down the list, we can find the next perfect number. We know that the next perfect number won't be prime since their only proper divisor is 1, so we can skip those. We then check the next composite number after 6, which is 8. The proper divisors of 8 are 1, 2, and 4. Sadly, we see that 8 is not perfect at all since 1 + 2 + 4 = 7.

Going right down the line like Gerry Rafferty, we find that the next perfect number is 28 since the sum of its proper divisors is 1 + 2 + 4 + 7 + 14 = 28. As is turns out, Euclid proved that 

2^p−1(2^p−1) is an even perfect number if 2^p−1is prime. Interestingly, it is not known whether any odd perfect numbers exist. However, Euler showed that, if an odd perfect number exists, it must be of the form

for the distinct odd primes p and qs, where 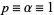 (mod 4). For a more thorough and interesting discussion of perfect numbers, see this wolfram page.

Another set of special numbers is the set of amicable numbers. Some of what follows is from the wolfram page covering this topic. We learned that these numbers come in pairs, whose proper divisors sum to one another. The example we saw in class is the pair 220 and 284. This is because the sum of the divisors of 220 is

1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284,

while the sum of the divisors of 284 is

1 + 2 + 4 + 71 + 142 = 220.

Other pairs include a pair credited to Fermat, 17 266 and 18 416, and a pair credited to Descartes, 9 363 584 and 9 437 056; however, both these pairs were known to Arab mathematicians at an earlier date.

A mathematician by the name of Thabit produced a method for finding pairs of amicable numbers, as you recall from class, which was rediscovered by both Fermat and Descartes. Euler then extended the method, stating that the numbers 2ⁿpq and 2ⁿr are amicable if

are prime for some integer 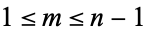. This extension, like Thabit's method, does not give us every amicable pair. Instead, these methods give sufficient, but not necessary, conditions for finding pairs of amicable numbers. With the advent of computers, the search for amicable pairs has become much more efficient, and there were over 12 million known amicable pairs as of 2007.

After some searching, I didn't find any useful applications of amicable numbers. It seems that they are simply an interesting result of our system of mathematics. Perhaps one day it could be used in the process of encryption, as many computers are certainly not powerful enough to calculate many of the amicable numbers that are continually being discovered.

We will now completely shift gears and return to the topic of the summation of sequences. Recall from my previous post that the sum x(n) of all natural numbers from 1 to n is given by the equation

x(n) = .5(n)(n + 1).

However, this formula was found simply by investigating the pattern the sums showed for various choices of n, and we have not yet proven that this is true. Well, the time has come. We will proceed with a proof by induction.

For the base case, notice that when n = 1, x(n) = 1. Thus, the base case holds and we assume the n = k case holds. That is, we will assume that

1 + 2 + ... + k = .5(k)(k + 1).

We will now show that the k + 1 case holds by showing

1 + 2 + ... + (k + 1) = .5(k + 1)[(k + 1) + 1)

                                                                  = .5(k + 1)(k + 2).

If we add the quantity k + 1 to each side of our induction hypothesis, we get

1 + 2 + ... + k + (k + 1) = .5(k)(k + 1) + (k + 1).

Removing a factor of .5 gives

1 + 2 + ... + k + (k + 1) = .5[(k)(k + 1) + 2(k + 1)].

Distributing gives us a pleasantly productive polynomial, producing

1 + 2 + ... + k + (k + 1) = .5(k² + 3k + 2).

At this time, we begin to lose our composure at the thought of factoring this polynomial. Our giddiness attracts the attention of our roommate, who long regretted signing a lease with us. Little does he know that we are staring at the final step of our proof. We finally write, with vehement confidence and satisfaction,

1 + 2 + ... + k + (k + 1) = .5(k + 1)(k + 2).

We have now shown that the sum of the natural numbers from 1 to n is x(n) = .5(n)(n + 1). Similar proofs can be written for the sum of squares and cubes, but these are exercises left for the reader. Proofs are always nice, since now we are certain that the formula we discovered earlier is true, even for ludicrous choices of n like 192,837,523,469,872 or 23,872,093,476,872,089,613,709,283,479,070,234. Plus, it's kind of fun to try to figure these things out knowing that they're likely true to begin with. Thank you for joining me in this adventure of the mind. See you next time.